Amazońscy Indianie odkrywają geometrię

"Nie mamy jednak w tej chwili żadnej pewnej teorii, która by to
wyjaśniała" - tłumaczy PAP współautor opublikowanych w najnowszym
"Science" badań, prof. Stanislas Dehaene z paryskiego College de
France.

W Platońskim dialogu "Menon" Sokrates pragnie udowodnić, że
wiedza jest wrodzona, a wszelkie uczenie się jest jedynie
przypominaniem (anamnesis). Prosi więc niewykształconego
niewolnika o podawanie odpowiedzi z dziedziny geometrii, które nie
wymagają wiedzy, a jedynie myślenia dedukcyjnego.

Nieco podobny eksperyment postanowili przeprowadzić naukowcy
francuscy i amerykańscy. W tym celu wybrali się do serca
brazylijskiej dżungli, nad rzekę Kururu, gdzie, odcięci od
cywilizacji, żyją Indianie z plemienia Munduruku. Indianie ci nie
posiadają w swoim języku słów oddających pojęcia geometryczne.
Okazuje się jednak, że posiadają trafne intuicje z dziedziny
geometrii euklidesowej.

"Co oznaczają takie pojęcia, jak +punkt+, +linia+, +równoległy+,
+kwadratowy+, +prostopadły+? Wszystko to są pojęcia idealne,
niespotykane w fizycznej rzeczywistości" - wyjaśnia Delhaene.
Okazuje się, jednak, że mimo to są uniwersalne kulturowo.

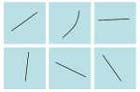
Badacze przeprowadzili szereg testów wśród Indian, zarówno wśród
dzieci, jak i dorosłych. Przedstawiano im na przykład sześć
obrazków, na pięciu były linie proste, na szóstym zaś krzywa.
Indianie musieli wybrać taki, który nie pasował do reszty.
Ponieważ Munduruku nie posiadają odpowiednich słów w swoim języku
do opisania obrazków, musieli jeden z nich nazwać "dziwnym" lub
"brzydkim".

Inny test polegał na przedstawieniu na prostej mapie-diagramie
trzech pojemników ustawionych w trójkąt. Tylko jeden z nich
zawierał jakiś przedmiot. Zadanie polegało na wskazaniu
odpowiadającego mu pojemnika w otoczeniu.

Grupę kontrolną stanowili Amerykanie - również dzieci i dorośli.
O ile dzieci indiańskie i amerykańskie wykazywały podobną trafność
odpowiedzi, o tyle dorośli Indianie byli gorsi w porównaniu z
dorosłymi Amerykanami - tutaj decydującym czynnikiem okazywało się
doświadczenie.

"Nasze badania sugerują, że te intuicje geometryczne są
niezależne od języka. Być może istnieje jakiś +instynkt
przyswajania geometrii+, tak jak prawdopodobnie istnieje +instynkt
nauki języka+. Jednak spekulacje te są w tej chwili przedwczesne,
ponieważ mamy niewiele dowodów na ten temat" - wyjaśnia PAP prof.
Dehaene.

Jak dodaje, badacze nie mają w tej chwili żadnej pewnej teorii,
która by to wyjaśniała. "Wiemy z badań na zwierzętach, że mózg
zawiera wiele map przestrzennych i ma wyczucie symetrii. Mamy
również piękny dowód, w przypadku liczb, że zaangażowany jest w
nie specyficzny obszar mózgu i że pojedyncze neurony związane są z
liczbami" - tłumaczy PAP Dehaene.

"Jednak kiedy chodzi o sieci neuronów, które kodują abstrakcyjne
pojęcia, takie jak +trójkąt równoboczny+, nikt nie wie, jak to
kodowanie się odbywa, a już w ogóle, jak mogą się te pojęcia
spontanicznie rozwijać" - dodaje.

Jednak, jak zastrzega badacz, "Należy zauważyć, że nasza praca
nie wykazuje, że wiedza geometryczna jest wrodzona. Najmłodsze
osoby, które badaliśmy, miały pięć lat, co sprawia, że mogły nabyć
tę wiedzę w uporządkowanym otoczeniu".

Naukowcy kontynuują swoje badania. "Współautor badań, Pierre
Pica, przebywa w tej chwili w Amazonii i przeprowadza wiele nowych
eksperymentów. Jedno z kluczowych pytań, które teraz postawiliśmy
i które - jak sądzę - spodobałoby się Riemannowi, Gaussowi czy
Kantowi - brzmi: czy ta podstawowa wiedza geometryczna skłania się
ku euklidesowej geometrii, czy może mamy również intuicje
nieeuklidesowe?" - podsumowuje profesor.(PAP)